Tổng Hợp Công Thức Lượng Giác Cơ Bản Và Nâng Cao| Bản Đầy Đủ

Các em thân mến, hôm nay chúng ta sẽ được ôn tập các kiến thức liên quan đến chuyên đề lượng giác. Như các em đã biết rằng, trong kỳ thi đại học, câu lượng giác là một trong những câu mặc định. Và thông thường thì các công lượng giác đó người ta sẽ hỏi vào phần phương trình lượng giác.

Bài Viết sau đây chúng tôi xin hệ thống lại các kiến thức từ cơ bản đến nâng cao của phương trình lượng giác, để qua đó giúp các em học sinh có một kỳ thi đạt được kết quả cao.

Phương trình lượng giác được đánh giá là câu hỏi dễ, và nhiệm vụ của chúng ta là phải hoàn thành hết các câu hỏi liên quan đến lượng giác và lấy điểm tối đa. Vậy để hoàn thành được câu lượng giác trong đề thi, các em nên nắm vững các công thức lượng giác từ cơ bản đến nâng cao. Việc các bạn học thuộc các công thức lượng giác là bạn đã hoàn thành 30% đề thi đại học. Dễ dàng nhận thấy rằng, đề thi đại học trong 10 năm trở lại đây, các câu lượng giác không có tính lắt léo, không có tính đánh đố mà chỉ thực hiện 1 nguyên tác hết sức đơn giản gặp gì biến đổi đó. Vậy thì vấn đề quan trọng là phải thuộc công thức, khi chúng ta thuộc công thức thì sẽ biến đổi rất tự tin và chính xác.

Trước khi học bài mới, các em có thể ôn tập bài cũ các công thức logarit

Các Công Thức Lượng Giác Cơ Bản Và Nâng Cao

Mô hình hiện đại trừu tượng hóa của lượng giác- lượng giác hữu tỷ, bao gồm các khái niệm “bình phương sin của góc” và “bình phương khoảng cách” thay vì góc và độ dài – đã được tiến sĩ Norman Wildberger ở trường đại học tổng hợp New South Wales nghĩ ra.

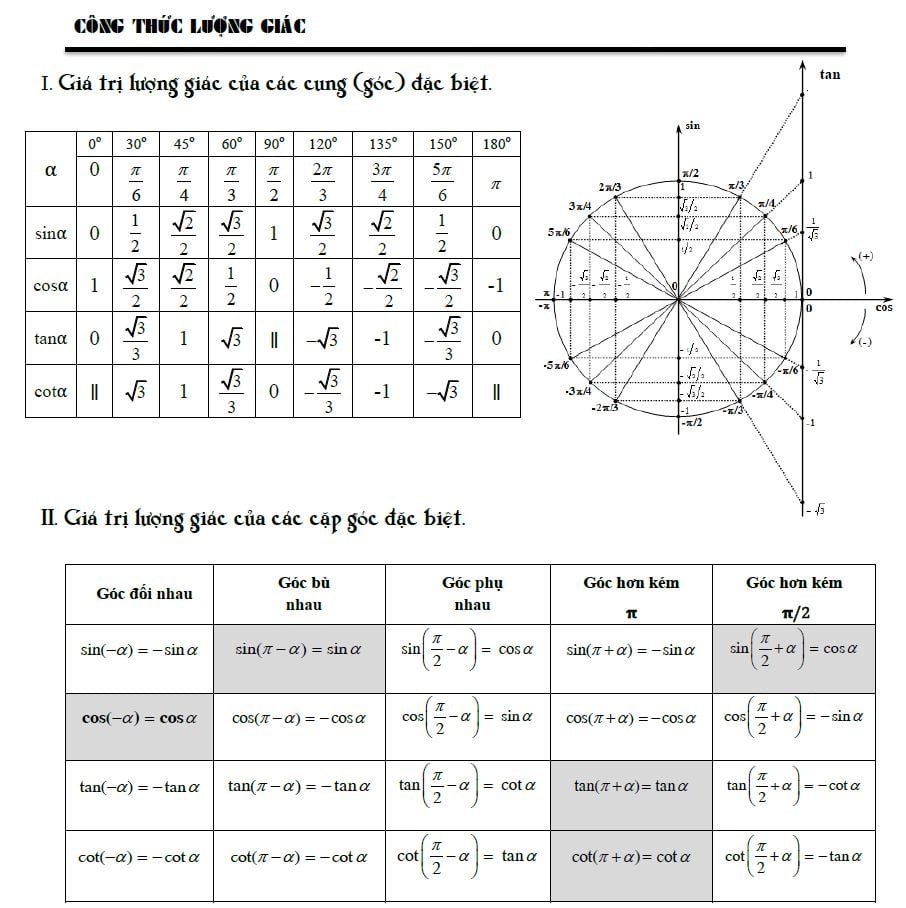
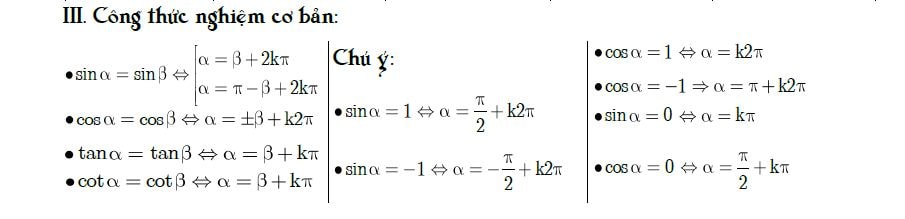
Xem video hướng dẫn học thuộc nhanh các công thức lượng giác cơ bản và nâng cao:

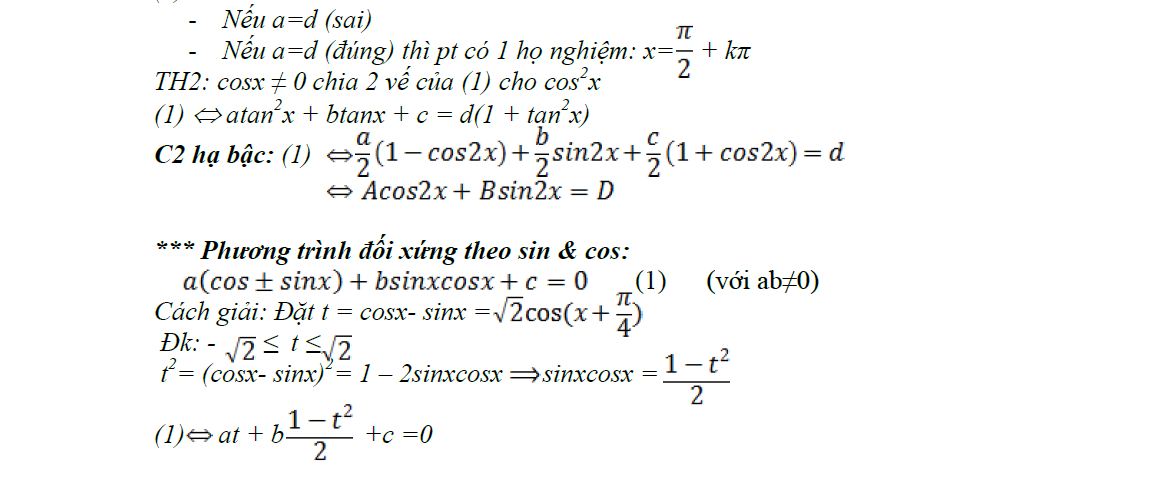
Sử dụng máy tính cầm tay giải nhanh trắc nghiệm lượng giác – Trần Anh Khoa

Nội dung tài liệu:
Phần I. Sử dụng máy tính cầm tay trong các bài toán góc và cung lượng giác
Phần II. Sử dụng chức năng calc của máy tính cầm tay để kiểm tra các đáp án
+ Dạng toán 1. Kiểm tra một giá trị là nghiệm của phương trình
+ Dạng toán 2. Kiểm tra một họ là nghiệm của phương trình
+ Dạng toán 3. Kiểm tra một tập là txđ của hàm số lượng giác
Phần III. Sử dụng máy tính cầm tay hỗ trợ giải phương trình bậc nhất đối với sinx và cosx
Phần IV. Sử dụng chức năng table của máy tính cầm tay
+ Dạng toán 1. Tìm gtnn và gtln của hàm số lượng giác
+ Dạng toán 2. Tìm chu kì tuần hoàn của hàm số lượng giác
+ Dạng toán 3. Xét tính đồng biến, nghịch biến của hàm số lượng giác
+ Dạng toán 4. Tìm nghiệm và số nghiệm của phương trình lượng giác trong một khoảng cho trước
Bài tập củng cố: chuyên đề sử dụng máy tính cầm tay giải nhanh trắc nghiệm lượng giác

XEM TÀI LIỆU ONLINE

Trong quá trình các em ôn thi nếu gặp vấn hoặc cần sự trợ giúp từ các gia sư thì có thể tham khảo bài viết sau nhé:

XEM KHOÁ HỌC: Học cùng gia sư luyện thi đại học tại nhà TPHCM

Trên đây là bài chia sẽ về kiến thức lượng giác, hi vọng rằng với những kiến thức mà chúng tôi đã chia sẽ, sẽ giúp bạn đạt điểm cao trong kỳ thi toán 10, toán 11, toán 12 và kỳ thi đại học sắp tới.

Trong trường hợp, các em bị hổng kiến thức quá nhiều không thể tự mình có thể giải các bài toán lượng giác hoặc các bài tập khác, các em có thể liên hệ với trung tâm nhờ trung tâm hỗ trợ tìm người dạy kèm tại nhà. Hay các trường hợp đang là học sinh TOP đầu trong lớp, và muốn bứt TOP thì việc tìm gia sư tại nhà hiệu quả không!

Bạn thân mến, việc học hiệu quả hay không phụ thuộc rất nhiều vào sự nỗ lực và cố gắng của bạn. Chúng tôi với nhiệm vụ giúp bạn tìm những giáo viên tốt nhất để giúp bạn định hướng học tập tốt nhất.

Thay vì đi đường vòng, hãy để GIA SƯ TRÍ VIỆT dẫn lối bạn!

Chúc bạn thành công.