Định Lý Viet
Chào bạn!
Trước khi vào bài học hôm nay thì tôi muốn tặng bạn một MẸO NHỎ giúp bạn tìm tại liệu hiểu quả.
Khi muốn tìm bất kỳ một tài liệu nào chỉ cần vào google.com.vn và gõ “từ khóa + gia sư trí việt” là sẽ ra kết quả bạn tìm kiếm.
Ví dụ: Bạn cần tìm công thức lượng giác thì bạn chỉ cần vào google và gõ công thức lượng giác gia sư trí việt thì sẽ có kết quả trả về là tài liệu từ gia sư Trí Việt.
Trở lại với bài học ngày nay, mời các bạn tìm hiểu về ĐỊNH LÝ VIET
Trong toán học, định lý Viète hay công thức Viète (có khi viết theo phiên âm tiếng Việt là Vi-ét), do nhà toán học Pháp François Viète tìm ra, nêu lên mối quan hệ giữa các nghiệm của một phương trình đa thức (trong trường số phức) và các hệ số của nó.

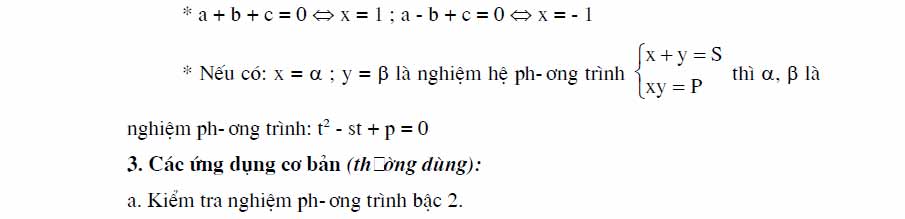



B. Các Ứng Dụng Của Định Lý Viet
I> Tìm Số Biết Tổng Và Tích Của Chúng.
-
Phương Pháp: Dựa Vào Định Lý Đảo Của Viet:




II> Tính giá trị các biểu thức đối xứng giữa các nghiệm
- Biểu Thức Đối Xứng Của 2 Nghiệm:
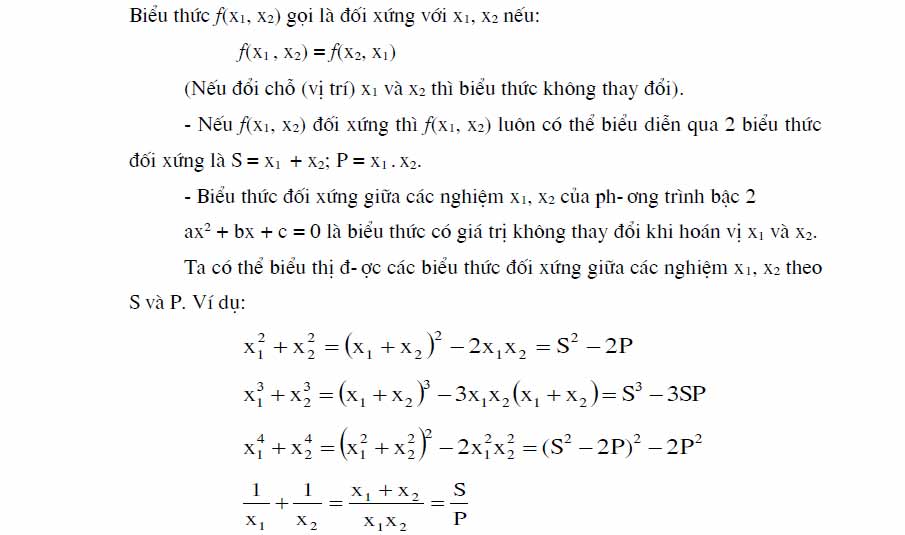

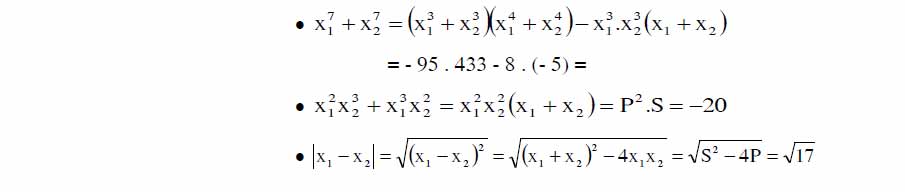



III> Tìm Hệ Thức Liên Hệ Giữa Các Nghiệm Phụ Thuộc Tham Số:
- Phương Pháp:


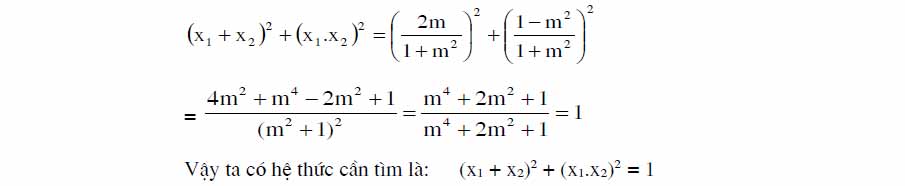
IV> Tìm Điều Kiện Của Tham Số Để 2 Nghiệm Liên Hệ Với Nhau Bởi 1 Hệ Thức Cho Trước (Điều Kiện Cho Trước)
1: Phương Pháp
Các Bước Thực Hiện



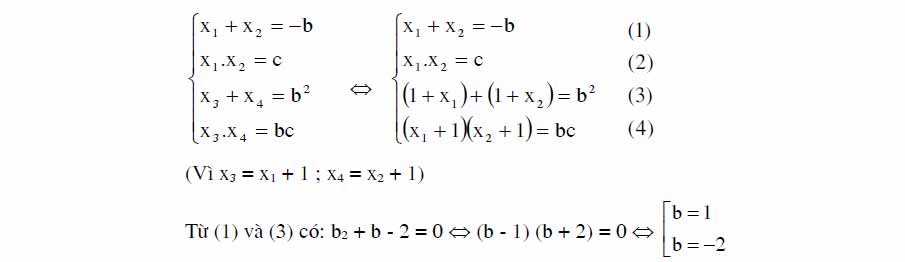

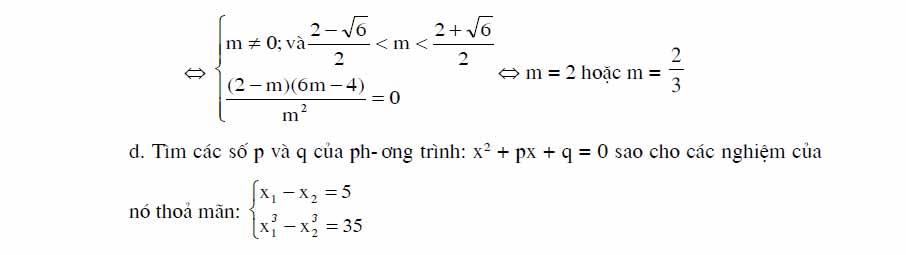

V. Thiết Lập Phương Trình Bậc 2
Ta thiết lập 1 phương trình bậc 2 nhận các số x1, x2 là các nghiệm dựa trên cơ sở (định lý viet)
Nếu x1+x2=S; x1.x2=P thì x1, x2 là nghiệm của phương trình
x2 – Sx + P = 0 (S2 – 4P >= 0)
Các Ví Dụ:



VI> Xét Dấu Các Nghiệm
- Phương Pháp:





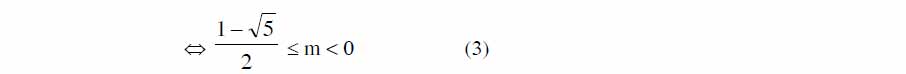
ỨNG DỤNG KHÁC
Phương Trình Đường Thẳng (D): Y= AX+B Với A khác 0 và y=mx với m khác 0
Dạng 1:














Tham khảo thêm về định lý viet
Trên đây là những chia sẽ từ Trung Tâm Gia Sư Trí Việt gửi tới bạn. Nếu gặp vấn đề nào khó ĐỪNG NGẦN NGẠI liên hệ với chúng tôi qua pages để hỗ trợ tốt hơn.
Trong trường hợp không giải quyết được bằng một vài tin nhắn. Chúng tôi sẽ gửi gia sư đến trực tiếp tại nhà hỗ trợ giúp bạn.
GIA SƯ TRÍ VIỆT – NÂNG TẦM TRI THỨC

hay
hay