Chu Vi Và Diện Tích Hình Tròn

28 Tháng Tám, 201723 Tháng Tám, 2018 Gia Sư Trí Việt 1795 Views 0 Comments

Trong loạt series chia sẽ kiến thức từ Trung Tâm Gia Sư Trí Việt, bài viết hôm nay chúng tôi sẽ chia sẽ kiến thức toán cơ bản về hình tròn. Nhằm giúp bạn đọc hiểu thế nào là hình tròn, cách tính chu vi, và diện tích hình tròn để từ đó các bạn vận dùng vào giải bài tập nhanh chóng nhất có thể.

Tóm tắt nội dung

Khái Niệm Hình Tròn.

Trong hình học phẳng, một hình tròn là một vùng trên mặt phẳng nằm “bên trong” đường tròn. Tâm, bán kính và chu vi của hình tròn chính là tâm và bán kính của đường tròn bao quanh nó.

Một hình tròn được gọi là đóng hay mở tùy theo việc nó chứa hay không chứa đường tròn biên.

Công Thức Hình Tròn.

Trong hệ tọa độ Descartes, hình tròn mở có tâm tại (a, b) và bán kính r là tất cả các điểm (x, y) thỏa mãn:

(x – a)² + (y – b)² < r²

Hình tròn đóng có tâm tại (a, b) và bán kính r là tất cả các điểm (x, y) thỏa mãn:

(x – a)² + (y – b)² ≤ r²

Hình tròn đơn vị

Khi bán kính của hình tròn là 1, hình tròn được gọi là hình tròn đơn vị hay đĩa đơn vị (hoặc dĩa đơn vị).

Chu vi hình tròn

Chu vi hình tròn hay đường tròn là đường biên giới hạn của hình tròn. Công thức của chu vi hình tròn là lấy đường kính nhân với pi hay 2 lần bán kính nhân pi.

Công thức của chu vi hình tròn là:

C=d\times pi

Hoặc có thể là:

C=r\times 2\times pi

Trong đó:

C là chu vi của hình tròn;
d là đường kính hình tròn;
r là bán kính hình tròn.

Quan hệ với Pi

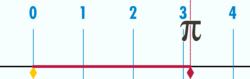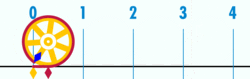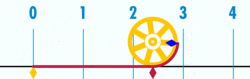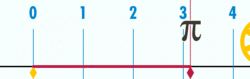
Chu vi của hình tròn liên quan với Pi. Giá trị của Pi là 3,141592653589793…. (xem Pi), được quy ước với giá trị gần đúng là 3,14.^[1] Pi được định nghĩa là tỷ lệ của chu vi

C

Các hằng số π được sử dụng phổ biến trong toán học, kỹ thuật và khoa học. Trong khi nó được đặt tên trong toán học thì kỹ thuật và khoa học nó không được đặt tên. Nó được sử dụng bởi radio, lập trình máy tính và hằng số vật lý.

Diện tích hình tròn

Diện tích hình tròn là diện tích của một hình tròn. Công thức của diện tích hình tròn là $S=\pi r^{2}$ với r là bán kính.

Diện tích của hình tròn đã được nghiên cứu bởi người Hy Lạp cổ đại. Eudoxus của Cnidus trong thế kỷ thứ 5 TCN đã tìm thấy rằng diện tích hình tròn là tỷ lệ thuận với bình phương bán kính của nó. Archimedes sử dụng các công cụ của hình học Euclide thấy rằng diện tích một hình tròn là tương đương với một tam giác vuông với chiều dài bằng chu vi hình tròn và chiều cao bằng bán kính của hình tròn.

Sử dụng trong đa giác

Diện tích của một đa giác đều bằng một nửa chu vi của nó nhân với chiều dài đường trung đoạn của đa giác đều. Khi số lượng các cạnh của đa giác tăng lên, đa giác có xu hướng trở thành một hình tròn và các đường trung đoạn có xu hướng trở thành bán kính của hình tròn đó.

Mở rộng

Hình tròn được mở rộng ra cho không gian ba chiều thành hình cầu, thể tích nằm trong mặt cầu.

Không gian Euclid n chiều, một hình tròn n chiều (hay đĩa n chiều) bán kính r là tất cả các điểm có khoảng cách tới một tâm cố định nhỏ hơn (với hình tròn mở) hay nhỏ hơn hoặc bằng (với hình tròn đóng) bán kính r. Một hình tròn n-1 chiều cũng là hình chiếu của hình cầu n chiều xuống một mặt phẳng n-1 chiều.

Các hình tròn đơn vị n chiều, ký hiệu, Dⁿ (hay Bⁿ) có tâm tại tâm hệ tọa độ và bán kính bằng 1.

Trên đây là những kiến thức mà đội ngủ gia sư Trí Việt muốn chia sẽ cho quý độc giả, hi vọng với những kiến thức mà chúng tôi chia sẽ, có thể giúp bạn đọc giải quyết được vấn đề đang gặp phải. Nếu có thắc mắc trong quá trình học tập bạn có thể đến trực tiếp tại văn phòng trung tâm gia sư Trí Việt để được giải đáp tốt nhất.